Example : we want to know influence of a new medicine on patients heart rate. We proceed a sampling of patients for whom we measure heart rate (Measure T0). Then we measure their heart rate a second time, after après le treatment of this new medicine (Measure T1). Since we measure twice the same parameter with the same subjects, measures are not independent, but dependant, or paired. The goal of our study is to compare the 2 heart rate means in order to know if gap between both means is significant or simply due to chance.
1 - Principes of t-test for comparison of 2 means from one subjects group (dependent groups) :
We have 2 samples a and b wose means (ma and mb) and variances (s²a and s²b) are estimators of means (µa and µb) and variances (θ²a et θ²b) of the 2 populations A and B from which samples are extracted. The question is : if ma and mb are different (which is easy to check), is it the same for µa and µb ?
- Null hypothesis : "H0 = µa and µb are equal"
- Alternative hypothesis : "H1 = µa and µb are different"
As both samples come from a unique group of subjects, analysis is different from t-test for independant groups where samples were independant. In this new case, each measure from sample a is connected to its homologue from sample b. Principle of the test consists in calculation, for each pair of measure, of the difference between values. Then, calculation of t-test for dependent groups consists in comparison of these differences mean (md) with 0 from which md must be close if both samples are from a unique population.
Hypotheses are changing in :
- Null hypothesis : "H0 = md is equal to 0
- Alternative hypothesis : "H1 = md is different from 0"
- In case of great effectives, we compare Z value with the limit value from the Z statistic table :
- In case of small effectives, we compare t value with the limit value from the Student table with df = n - 1 :
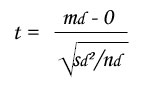
- Conditions to use the test (automatically checked by StatEL) :
- normal distribution of the differences between both means
2 - Launch of t-test for comparison of 2 means from one subjects group (dependent groups) :
StatEL requires you to select the cells range related to the first studied group, then it needs you to select the cells range related to the second group of subjects. To proceed the selection, you just have to clic on the first cell of your data with the mouse and to stretch until the last cell of your data.
Nota bene : in order to identify at the best different measures groups, first cell of each selection must contain name of the group. These names will be used in the results sheet.
Nota bene : in t-test for dependent groups, number of measures is supposed to be the same for each group. However, StatEL will manage missing data if, for each group, selection is applying on exactly the same number of cells (empty or not).
3 - Results of t-test for comparison of 2 means from one subjects group (dependent groups) :
Results display on a new sheet of you Excel file :
- On the left part of the sheet, you can see table of selected data.
- On the right part of the sheet are displayed table of descriptive statistics, tested hypotheses, results of t-test calculation, and t-test's conclusions. If results allow to reject H0 hypothesis, i.e. if means of both groups are significantly different, conclusions as well as p-value are written in red.
- If conditions of t-test are not respected, a red warning message is written, as well as the name of the nonparametric test analogous to the t-test that you can use to perform a correct statistical analysis.
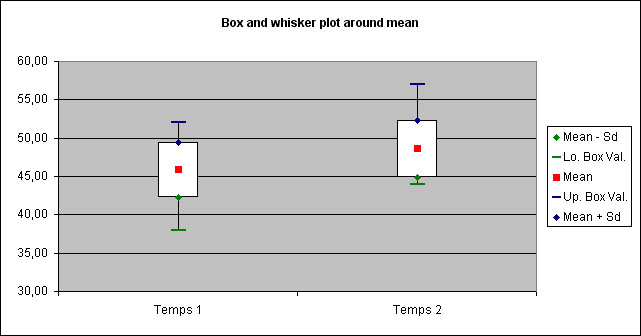
In the mentioned example, StatEL explains clearely that means of the 2 groups are significantly different, with a p-value (risk to make a mistake) lower than 0,0045.
It is also specified that conditions of the test are respected (conditions checked with StatEL, transparently for the user) ; the user can thus trust results.
A "Whiskers plot" is displayed to illustrate results :
|