| |
This test is equivalent to parametric Anova for comparison of K means from dependent groups, but without requirement of sample distribution.
Example : we want to evaluate progression of a pupils group at school. We ask them to fill in 3 forms at 3 different times and we compare means of marks resulting from the 3 forms. However, preliminary analysis revealed that normal distribution of measures was not respected. Then, utilization of ANOVA is not possible. We must resort the nonparametric Friedman test to compare the 3 means in order to know if gap between means is significant or simply due to chance
1 - Principles of Friedman test :
We have several samples (K>2) whose means (mi, mj, ...) and variances (s²i, s²j, ...) are estimators of means (µi, µj, ...) and variances (θ²i, θ²j, ...) of populations from which samples are extracted. The problem is : si mi, mj, ... are differents (which is easy to check), is it the same for µi, µj, ... ?
- Null hypothesis : "H0 : µi = µj = ..."
- Alternative hypothesis : "H1 : there is at least one mean that is different from the others"
In any nonparametric test, and on the contrary of parametric tests, calculation does not take into account numeric values of measures from samples representative of the populations. Nonparametric tests are based on ranks of values. Then we are free of normal distribution conditions and homogeneity of variances, indispensable for liability of parametric tests.
- We do not rank data by group (in columns), but by subject (in rows). Example : we study a group of 10 subjects exposed to 3 different conditions, we have then 10 triplets of measures (1 per subject) ; calculation of ranks is realized inside each triplet.
- We calculate sum of ranks (Rk) for each of the k groups.
- Then we calculate the F coefficient of Friedman :
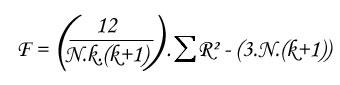
- If k < 6 or N < 14, we compare F to critical value issued from Friedman table.
- If k > 5 ou N > 13, F is compared to Chi² limit value with (k-1) df.
- There is no condition to use Friedman test (excepted aleatory sampling).
At the end of Friedman test, StatEL resort a post-hoc test in order to define conclusions in case of rejection of H0. Indeed, Friedman test does not allow to specify which mean(s) is (are) different from the others.
Then, we proceed the "method of ranked means". This test consists in ranking means of different studied groups in rising order. We compare pair of contiguous means thanks to Wilcoxon test. Thus, we proceede only (k-1) comparisons instead of the k(k-1)/2 possible comparisons.
At the end, we can have a result like : m5 = m1 < m4 < m3 = m2.
Note : it may happen that this posthoc test concludes no complementary information (m1 = m3 = m2) ; it hides the fact that difference is between m1 and m2 and not between m1 and m3 or between m3 and m2.
2 - Launch of Friedman test :
StatEL requires you to specify the number of different groups you want to compare. Then, you have to select successively the cells range related to each studied group. This dialog boxwill display as many time as the number of different groups to compare. To proceed the selection, you just have to clic on the first cell of your data with the mouse and to stretch until the last cell of your data.
Nota bene : in order to identify at the best different measures groups, first cell of each selection must contain name of the group. These names will be used in the results sheet.
Nota bene : in Friedman test, number of measures is supposed to be the same for each group. However, StatEL will manage missing data if, for each group, selection is applying on exactly the same number of cells (empty or not).
3 - Results of Friedman test :
Results display on a new sheet of you Excel file :
- On the left part of the sheet, you can see table of selected data.
- On the right part of the sheet are displayed table of descriptive statistics, tested hypotheses, results of Anova calculation, and Friedman test conclusions. If results allow to reject H0 hypothesis, i.e. if at least one mean is significantly different, conclusions as well as p-value are written in red.
In the mentioned example, StatEL explains clearely that at least one mean is significantly different, with a p-value (risk to make a mistake) lower than 0,01.
A "Whiskers plot" is displayed to illustrate results :
|